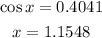Question

Two students were playing the same game. The difference in points leading score of the game can be modeled by the function Y=5sin x+3 sin x cos x. Within the interval 0

Answer 1

Step 1

Interprete the range of x

The range is 0

This means that x>0 but x<6

Step 2

Differentiating y with respect to x, we have

`\begin{gathered} (dy)/(dx)=5\cos x+3(\sin x(-\sin x)+\cos ^2x) \\ (dy)/(dx)=5\cos x+3(\cos ^2x-\sin ^2x)=5\cos x+3\cos 2x \\ (d^2y)/(d^2x)=-5\sin x-6\sin 2x \end{gathered}`

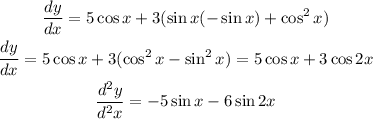
Step 3: Find the stationary point,

At the stationary points, we have

`\begin{gathered} 5\cos x+3(\cos ^2x-\sin ^2x)=0 \\ 5\cos x+3(2\cos ^2x-1)=0 \\ 6\cos ^2x+5\cos x-3=0 \end{gathered}`
`\text{Let m }=\cos x`

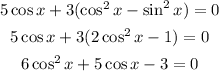
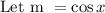
Then,

`\begin{gathered} 6m^2+5m-3=0 \\ m=-1.2374,\text{ or }0.4041 \end{gathered}`

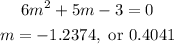
Since the values of cos x cannot be less than -1, then the only possibility is

`\begin{gathered} \cos x=0.4041 \\ x=1.1548 \end{gathered}`