We are told that the volumes between two spheres is 16/3, this means that:
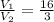
Now the formula for the volume of a sphere is:
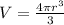
Replacing in the previous formula:

Simplifying:
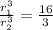
Now we solve for the first radius which is the radius of the bigger sphere:
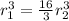
Now we determine the radius of the smallest ball using the formula for the surface area of a sphere:
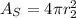
Now we replace the value of the surface area:

Now we solve for the radius:
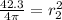
Taking square root on both sides:
![\sqrt[]{(42.3)/(4\pi)}=r_2](https://img.qammunity.org/2023/formulas/mathematics/college/47uu7ami6n9f6egtxgdbzpkh7v750co8h1.png)
Solving the operation:
![1.83\operatorname{cm}=r_2]()
Now we replace the value of the radius in the proportion:
![r^3_1=(16)/(3)(1.83\operatorname{cm})^3]()
Solving the operations:
![r^3_1=32.7\operatorname{cm}^3]()
Taking cubic root to both sides:
![r_1=\sqrt[3]{32.7\operatorname{cm}^3}]()
Solving the operation:
![r_1=3.19\operatorname{cm}]()
Now we use the formula for the surface area using the new radius:

Replacing the radius:
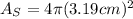
Solving the operation:
![A_S=127.9\operatorname{cm}^2]()
Therefore, the surface area of the new ball is 127.9 square centimeters.