Question

5. In places where there are crickets, the outdoor temperature can bepredicted by the rate at which crickets chirp. One equation that models the relationship between chirps and outdoor temperature is f = 1/40 + 40, where cis the number of chirps per minute and f is the temperature in degreesFahrenheit5a. Suppose 110 chirps are heard in a minute. According to this model, whatis the outdoor temperature?5b. If it is 75 outside, about how many chirps can we expect to hear in oneminute?5c. The equation is only a good model of the relationship when the outdoortemperature is at least 55. (Below that temperature, cric aren't aroundor inclined to chirp.) How many chirps can we expect to hear in a minute atthat temperature?

Answer 1

Given the relationship

`\begin{gathered} f=(1)/(4)c\text{ + 40} \\ \end{gathered}`

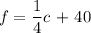
Where f = the temperature in degrees Fahrenheit

c= the number of chirps per minute

A.

Given that c=110,

Substitute c=110 into the equation above, we have

`\begin{gathered} f=(1)/(4)(110)\text{ + 40} \\ f=27.5\text{ + 40} \\ f=67.5 \end{gathered}`

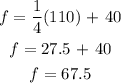
The outdoor temperature is 67.5 degrees fahrenheit

B.

If it is 75 outside, about how many chirps can we expect to hear in one

minute?

f = 75. c = ?

Substitute f = 75 into the relationship

`\begin{gathered} 75=(1)/(4)c\text{ + 40} \\ \text{ multiply through by 4} \\ 300=c\text{ + 160} \\ c=300-160 \\ c=140 \end{gathered}`

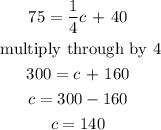
Hence, If it is 75 outside, we expect to hear 140 chirps in one minute

C.

When the temperature is 55 degrees fahreheit,

f = 55

`\begin{gathered} 55=(1)/(4)c\text{ + 40} \\ mu\text{ltiply through by 4} \\ 220=c+160 \\ c=220-160 \\ c=60 \end{gathered}`

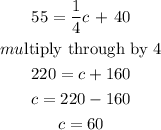
Hence, at this temperature (55) we can expect to hear 60 chirps in one minute

D.

1/4 means the slope in the relationship. That is, the rate of change of temperature with respect to number of chirps per minute

E.

40 tells us the initial temperature when the number or chirps heard per minute is zero.