We have to identify the outliers of this data set.
We can start by sorting the elements:
89.19.19.19.29.49.49.810.711.9
We have two values that can be considered outliers (8 and 11.9). To find if they are outliers or not, we calculate the mean and the standard deviation to see how far from the mean are this extreme values.
We start calculating the mean as:
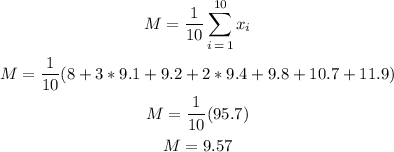
Now, we can calculate the variance as (NOTE: then we can calculate the standard deviation from the variance by applying the square root):
![\begin{gathered} s^2=(1)/(10-1)\sum_(i=1)^(10)(x_i-M)^2 \\ s^2=(1)/(9)[(8-9.57)^2+3*(9.1-9.57)^2+(9.2-9.57)^2+2*(9.4-9.57)^2+(9.8-9.57)^2+(10.7-9.57)^2^+(11.9-9.57)^2] \\ s^2=(1)/(9)(2.4649+3*0.2209+0.1369+2*0.0289+0.0529+1.2769+5.4289) \\ s^2=(1)/(9)(10.081) \\ s^2\approx1.12 \end{gathered}]()
Then, the standard deviation will be:
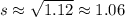
We can use the rule of the 3 sigmas: if the data point is at a distance that is more than 3 standard deviations from the mean, it can be considered an outlier.
Then, we check the limits that this 3 standard deviations impose:
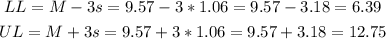
As all of the data points are within this limits, we can not label any of the points as outliers.
Answer: None of the above (Option D)