Question

The overhead reach distances of adult females are normally distributed with a mean of 205.5 and a standard deviation of 7.8 cm.

Answer 1

Answer: (a) P(x>214.80)= 0.88

(b) P( x >204.20 ) = 0.74

(c) population is normally distributed , hence we can apply the normal distribution in part b even though sample size <30 .

Explanations :

given :

`\begin{gathered} \mu\text{ = 205.5 } \\ \sigma\text{ = 7.8 } \end{gathered}`

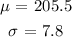
(a) P(x>214.80) :

`\begin{gathered} \Rightarrow p(\frac{x\text{ - }\mu}{\sigma}) \\ \text{ = }P\text{ (Z > }\frac{214.80\text{ - 205.5}}{7.8\text{ }}) \\ \text{ = }P(Z\text{ >1.185 )} \\ \text{ = 1 - }P(Z\leq1.185) \\ \text{ = 1 -0.11}80\text{ } \\ =\text{ 0.88} \end{gathered}`

This means that the probability that individual distance is greater than 214.8 = 0.88 or 88%

(b) P( x >204.20 ) :

`\begin{gathered} P\text{ ( }\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}}>\text{ }\frac{204.20\text{ - 205.5}}{\frac{7.8\text{ }}{\sqrt[]{15}}}\text{ )} \\ =\text{ P(z> -0.645)} \\ =\text{ 1 - P( z >-0.645)} \\ =\text{ 1-}0.2594 \\ =0.74 \end{gathered}`

• This means that the probability of distance greater than 204.20 = 0.74 or 74%

(c) We were told that the population is normally distributed , hence we can apply the normal distribution in part b even though sample size <30 .