Let l, x, and h be the length, width, and height of the cuboid.
Therefore, its surface is given by the formula,
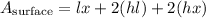
(Notice that the box does not have a lid.)
Furthermore,
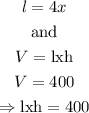
1) Notice that we have two conditions,
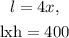
Therefore,
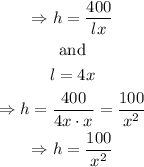
Therefore, the surface area as a function of the width is
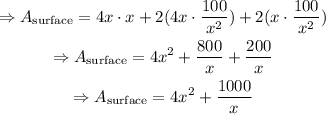
We need to find the minimum of the function above; first, derivate A_surface and solve A'(x)=0, as shown below

Then,
![\begin{gathered} A^(\prime)_{\text{surface}}(x)=0 \\ \Rightarrow8x-(1000)/(x^2)=0 \\ \Rightarrow8x^3-1000=0 \\ \Rightarrow x^3=(1000)/(8) \\ \Rightarrow x=\sqrt[3]{(1000)/(8)}=(10)/(2)=5 \\ \Rightarrow x=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1p4zn1nirci1votmjvgegues5uw8b3vp42.png)
Therefore, the width that minimizes the total surface area is x=5cm.
Finding l and h,
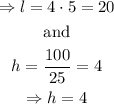
The answers to part a) are l=20cm, x=5cm, h=4cm.
b)
Finally, set l=20, x=5, and h=4cm in the A_surface function, as shown below,
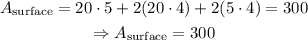
The minimum total surface area is 300cm^2