Question

The amount of pollutants that are found in waterways near large cities is normally distributed with mean 9.8 ppm and standard deviation 1.4 ppm. 12 randomly selected large cities are studied. Round all answers to 4 decimal places where possible.What is the distribution of X ? X ~ N(,)What is the distribution of ¯x ? ¯x ~ N(,)What is the probability that one randomly selected city's waterway will have less than 10.3 ppm pollutants? For the 12 cities, find the probability that the average amount of pollutants is less than 10.3 ppm. For part d), is the assumption that the distribution is normal necessary? YesNoFind the IQR for the average of 12 cities.Q1 = ppmQ3 = ppmIQR: ppm

Answer 1

Given:

population mean (μ) = 9.8 ppm

population standard deviation (σ) = 1.4 ppm

sample size (n) = 12 cities

Find the following:

a. distribution of X

The distribution of X follows the pattern X ~ N (μ, σ²). Since we know the population mean and population standard deviation already, let's plug it into the pattern mentioned.

`X-N(9.8,(1.4)^2)`

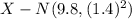
which is equivalent to X ~ N(9.8, 1.96).

b. distribution of the mean

We follow the same pattern however, we have to calculate the sample standard deviation using the standard error formula.

`s=(\sigma)/(√(n))\Rightarrow(1.4)/(√(12))\Rightarrow(1.4)/(3.464)\Rightarrow0.4041`

Square the standard error.

`0.4041^2\approx0.1633`

Hence, the distribution of the mean is bar x ~ N(9.8, 0.1633).

c. To determine the probability of one city having less than 10.3 ppm pollutants, let's convert 10.3 to a z-value first.

`z=(x-\mu)/(\sigma)`
`z=(10.3-9.8)/(1.4)=(0.5)/(1.4)=0.3571`

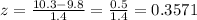
The equivalent z-value of 10.3 ppm is 0.3571. Let's plot this in the normal curve and shade the left side of it since we want to know "less than" 10.3 ppm.

Let's find the area of the shaded region. We know that half of the normal curve already has an area of 0.5. Now, let's find the area from the center to z = 0.3571 by referring to the standard normal distribution table.

Based on the table, the area from the center to z = 0.3571 is 0.1395.

Let's add 0.5 and 0.1395 to get the total area of the shaded region.

`0.5+0.1395=0.6395`

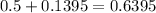
The area of the shaded region is 0.6395.

Hence, the probability that one random city has less than 10.3 ppm pollutants is 0.6395.

d. To determine the probability that the sample mean of 12 cities is less than 10.3 ppm, we follow the same steps above but our formula to convert 10.3 to z-value is different. See the conversion below.

`z=\frac{\bar{x}-\mu}{\sigma/√(n)}`
`z=(10.3-9.8)/(1.4/√(12))=(0.5)/(0.4041)=1.2372`

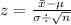
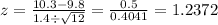
The equivalent z-value of the sample mean of 10.3 is 1.2372. Let's plot this in the normal curve and shade the left side of it since we want to know "less than" 10.3 ppm.

Similar to the process we have done in part c, let's find the area of the shaded region from the center to z = 1.2372 and add it to 0.5.

Based on the standard normal distribution table, the area from the center to z = 1.2372 is 0.3920.

`0.5+0.392=0.892`

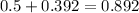
The area of the shaded region is 0.892.

Hence, the probability that the sample mean of 12 cities is less than 10.3 ppm is 0.8920.

e. Yes, the assumption that the distribution is normal is necessary.

f. Q1 covers 25% of the data on its left so, let's find the z-value that has an area of 0.25 on its left.

Based on the table, the z-value is -0.674. Let's multiply this by the sample standard error and add the result to the mean.

`-0.674*0.4041=-0.2724`
`-0.2724+9.8=9.5276`

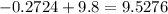
Hence, the Q1 value is 9.5276 ppm.

On the other hand, the Q3 covers 75% of the data on its left or 25% from the center. In this case, the equivalent z-value is 0.674.

Do the same process above.

`0.674*0.4041=0.2724`
`0.2724+9.8=10.0724`

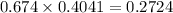
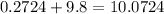
Therefore, the Q3 value is 10.0724 ppm.

To determine the IQR, simply subtract Q1 from Q3.

`10.0724-9.5276=0.5448`

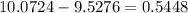
Therefore, the IQR for the average of 12 cities is 0.5448 ppm.