Question

How many revolutions will the tire have made after traveling one mile?

Answer 1

Step 1: Let's find the circumference of the tire in feet.

Given:

Recall: 1 foot = 12 inches

Radius = 13 inches = 13 ÷ 12 = 13/12 Feet

We get,

`\text{ Circumference = 2}\pi r`
`\text{ = 2}\pi((13)/(12))`
`\text{ Circumference = }(26)/(12)\pi\text{ = }(13)/(6)_{}\pi\text{ feet}`

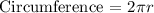
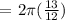
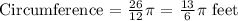
Step 2: Let's now determine the number of revolutions that tire will have in 1 mile.

`\text{ Total number of revolutions = }\frac{\text{ 1 mile}}{\text{ Circumference of the tire}}`

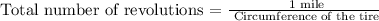
Recall: 1 mile = 5280 feet

We get,

`\text{ Total number of revolutions = }\frac{\text{ 5}280}{(13\pi)/(6)_{}}`
`\text{ = 5280 x }\frac{\text{ 6}}{13\pi}`
`\text{ = }\frac{\text{ 3}1680}{13\pi}`
`\text{= }\frac{\text{ 3}1680}{13\pi}\text{ = }(31680)/(13(3.1416))\text{ = 775.69489334195}`
`\text{ Total number of revolutions }\approx775.69\text{ }`

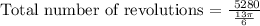
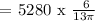
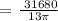
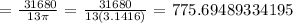
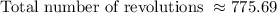
Therefore, the answer is 775.69 revolutions.