To answer this question we will use the following formula for binomial probability:
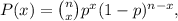
where x is the number of times for a specific outcome within n trials, and p is the probability of success on a single trial.
Substituting x=5, n=12, and p=0.44 in the above formula we get:
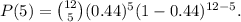
Simplifying the above result we get:
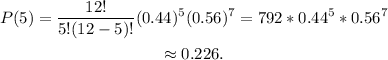
Answer: 0.226.