Given:
The quadratic equation is,
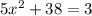
Step-by-step explanation:
Simplify the equation.
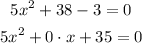
For the given equation a = 5, b = 0 and c = 35.
The quadratic formula is,
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Substitute the values in the equation to solve the equation.
![\begin{gathered} x=\frac{-0\pm\sqrt[]{(0)^2-4\cdot5\cdot35}}{2\cdot5} \\ =\frac{\pm\sqrt[]{-700}}{10} \\ =\frac{\pm10\sqrt[]{7}i}{10} \\ =\pm√(7)i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yjvjb8tzflolzcsitrrohcvosaefeipdxt.png)
Second method:
Solve the equation.
![\begin{gathered} 5x^2+38=3 \\ 5x^2=3-38 \\ x^2=-(35)/(5) \\ x=\pm\sqrt[]{-7} \\ =\pm\sqrt[]{7}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3albwjid19edju25ggh6t3sjz9xeapu0ds.png)
I prefer the second method for solving as quadratic equation donot have x terms, so it can be solved easily by combining the like terms.
If equation has x terms also and cannot split the middle terms then quadratic formula method is preffered.
Answer:
![\pm\sqrt[]{7}i](https://img.qammunity.org/2023/formulas/mathematics/college/gr1pade7dak3ufgd7dopqty990w0vvlp73.png)
Prefer second method as there are no x terms in quadratic equation, so it can be simplify easily by conbining like terms.