Given the information, we know that the groth is linear, and also we have two points: (2,4) and (5,5.5). Then we can find the equation in the following way:
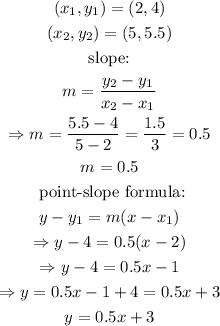
If h are the inches and n the weeks, then the equation is:
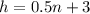
Now, if we want to know how tall will be the plant in 10 weeks, we just make n=10 and find the value of h:
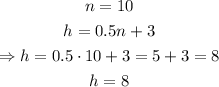
therefore, after 10 weeks, the plant will be 8 inches.
Finally, to find out how many weeks will it take the plant to grow 20 inches, we make h=20 and solve for n:
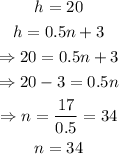
therefore, the plant will be 20 inches tall in 34 weeks