The four statements are true.
Let's see each one:
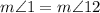
Since 1 and 12 are exterior angles, and are alternated; we can use the Alternate exterior angles theorem, which states that, given two parallel lines and one that crosses both, the opposite exterior angles that form the crossing line, are congruent. then this is true.
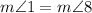
This is almost the same as the one before. in this case, we don't look at the line c. We only look at the lines a, b and the one transversal to them. Then, 1 and 8 are again opposite exterior angles. For the theorem, they're congruent.

In this case, we'll need a intermediate step to be able to apply the alternate angles theorem. We know that:
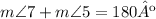
Because both form a straight line. Then we can use the consecutive angles theorem, which says that if two angles are consecutive (two angles formed by two parallels with a transversal) the two angles add to 180º. This means: