Answer:
• (4,-5)
,
• (-6,10)
Step-by-step explanation:
The coordinates of the endpoints of the line segment LM are (-8, 13) and (6, -8).
If point P divides LM into two parts with lengths in a ratio of 6:1.
Since the exact points, L and M are not given, we can switch the coordinates as desired.
• Taking L(-8, 13) and M(6, -8).
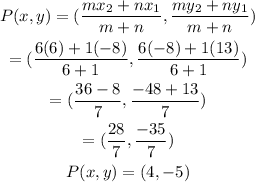
• Taking L(6, -8) and M(-8, 13)
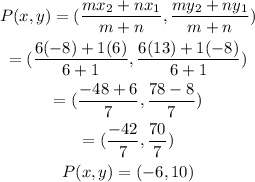
The two possible locations for point P are (4, -5) and (-6, 10).