Question

The following steps were used to prove 1. Factor.II. Simplify.III. Use a Pythagorean identity.IV. Use a quotient identity.V. Use a reciprocal identity.In which order were the steps performed?

Answer 1

Step 1

Write the trigonometric equation

`tan^2\theta\text{ - sin}^2\theta\text{ = sin}^4\theta sec^2\theta`

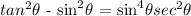
Step 2

Apply the quotient identity

`(sin^2\theta)/(cos^2\theta)\text{ - sin}^2\theta`

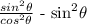
Step 3

Factor out the common factor

`sin^2\theta((1)/(cos^2\theta)-\text{ 1\rparen}`

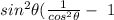
Step 4

simplify

`sin^2\theta((1-cos^2\theta)/(cos^2\theta))`

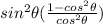
Step 5

Reciprocal identity

`sin^2\theta(1\text{ - cos}^2\theta)sec^2\theta`

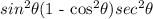
Step 6

Use the Pythagorean identity

`\begin{gathered} sin^2\theta\text{ + cos}^2\theta\text{ = 1} \\ sin^2\theta\text{ = 1 - cos}^2\theta \\ Hence \\ sin^2\theta(1\text{ - cos}^2\theta)sec^2\theta \\ sin^2\theta\text{ }*\text{ sin}^2\theta\text{ }*\text{ sec}^2\theta \end{gathered}`

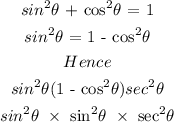
Step 7

Simplify

`sin^4\theta sec^2\theta`

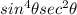
Final answer

Option D

IV , I , II , V , III , IV , II