Answer:
Given that,
An amount of $23,000 is borrowed for 11 years at 6.75% interest, compounded annually.
To find the Amount paid back after 11 years.
Step-by-step explanation:
we know that,
The formula to find the,
Amount after n years of interest rate r% compounded annually is,
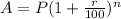
where P is the initial amount.
Here, we have that,
P=$23,000
r=6.75
n=11
Substitute the values we get,
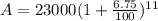
Solving this we get,
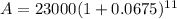
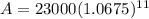
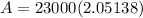
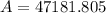
Round to the nearest dollar.
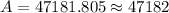
Answer is: Amount paid back is $47182 after 11 years