1)
Find f(1).
To find f(1) we must look at the "x" column, find "1", and then look at the "f(x)" on the same line.
Searching for x = 1, we can see that on the same line, f(x) = 1, that means f(1) = 1.

2)
Find f(9).
Using the same logic, we will search for "9" at the "x" column, after we find it we will look at the same line to the "f(x)" column. Looking at the table we can see that on the same line as 9 we have 3 at "f(x)" column. Therefore
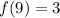
3)
Find f(4).
Again, search for "4" at "x" column, on the same line we have 2 at "f(x)" column, then
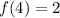
4)
Find f(____) = 0
Now we will do the inverse logic, we will look at "f(x)" column, find "0" and then look on the same line what is the value of "x". If we do that we can see that
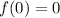
5)
if f(x) = 4, then x = ???
Now we will repeat the same process as 4), let's search for "4" at the "f(x)" column, it's the last line, on the last line the value of "x" is 16. Therefore
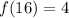
if f(x) = 4, then x = 16