Question

The first three terms of a geometric sequence are as follows. 4, 20, 100 Find the next two terms of this sequence. States 4, 20, 100,

Answer 1

Given the first three terms of a geometric sequence:

`\text{ 4, 20, 100}\ldots`

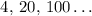
To be able to determine the next 2 terms, let's first find out their common ratio r.

`\begin{gathered} \text{ }(20)/(4)\text{ = 5} \\ \\ (100)/(20)\text{ = 5} \end{gathered}`

Therefore, the common ratio r is 5.

Let's find the next 2 terms:

a.) The 4th term.

`\text{ A}_4=A_1(r)^{n\text{ - 1}}=(4)(5)^{4\text{ - 1}}=(4)(5)^3`
`\text{ = (4)(125)}`
`\text{ A}_4\text{ = 500}`

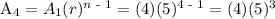
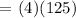
b.) The 5th term.

`\text{ A}_4=A_1(r)^{n\text{ - 1}}=(4)(5)^{5\text{ - 1}}=(4)(5)^4`
`\text{ = 4(625)}`
`\text{ A}_5\text{ = 2,500}`

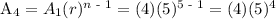
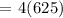
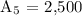
Therefore, the next 2 terms (4th and 5th) of the geometric sequence are 500 and 2,500 respectively.