Question

Find the quadratic equation whose roots are 5 and -5

Answer 1

Given the roots of the Quadratic Equation:

`\begin{gathered} x=5 \\ x=-5 \end{gathered}`

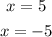
You can write the Quadratic Equation in Factored Form:

`(x-5)(x+5)=0`

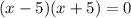
Now you need to multiply the binomials using the FOIL Method, which states that:

`\mleft(a+b\mright)\mleft(c+d\mright)=ac+ad+bc+bd`

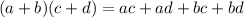
Then:

`(x)(x)+(x)(5)-(5)(x)-(5)(5)=0`
`x^2+5x-5x-25=0`

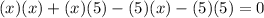
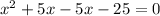
Adding the like terms, you get:

`x^2-25=0`

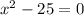
Hence, the answer is: Second option.