Question

Determine the perimeter of the perimeter of the following polygons

Answer 1

It is important to know that the perimeter is the sum of all sides.

We already know that the base of the triangle is 3 units long.

On the other hand, we have to use the distance formula to find the length of the other two sides.

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Let's find the length between the points (0,6) and (1,0), where

`\begin{gathered} x_1=0 \\ x_2=1 \\ y_1=6 \\ y_2=0 \end{gathered}`
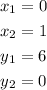
`\begin{gathered} d=\sqrt[]{(1-0)^2+(0-6)^2} \\ d=\sqrt[]{1+36}=\sqrt[]{37}\approx6.1 \end{gathered}`

Then, we find the length between the points (0,6) and (4,0).

`\begin{gathered} d=\sqrt[]{(0-6)^2+(4-0)^2} \\ d=\sqrt[]{36+16}=\sqrt[]{52}\approx7.2 \end{gathered}`

Once we have the length of all three sides, we add them to find the perimeter

`P=3+6.1+7.2=16.3`

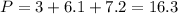
Hence, the perimeter is 16.3 units long.