Question

Which of the following functions would result in a graph that is shifted three units to the left

Answer 1

`c)f(x)=4\text{ log\lparen x+3\rparen}`

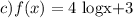
Step-by-step explanation

to shift a function left, add inside the function's argument: f(x + b) shifts f(x) b units to the left. Shifting to the right works the same way, f(x - b) shifts f(x) b units to the right.

Step 1

given

`f(x)=4\text{ log \lparen x\rparen}`

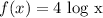
if the function is shifted three units to the left then

`\begin{gathered} b=3(positive) \\ \end{gathered}`

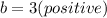
hence

`\begin{gathered} g(x)=4\text{ log \lparen x\rparen}\Rightarrow shifted\text{ 3 units to left}\Rightarrow g(x+3)\Rightarrow f(x) \\ add\text{ x to the argument of the function} \\ f(x)=4\text{ log\lparen x+3\rparen} \end{gathered}`

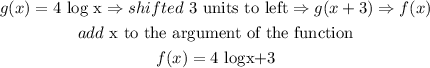
therefore, the answer is

`c)f(x)=4\text{ log\lparen x+3\rparen}`

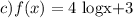
I hope this helps you