We will determine how much time it takes for Jenna to buy a guitar.
First we will try to analyze Jenna's bak account situation. She has a certain amount of savings ( S ) and she plans to save ( r ) amount every week.
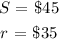
We will express the amount that Jenna has in ( x ) number of weeks in her saving account:
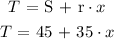
Jenna wants to buy a guitar which costs ( c ) around:
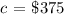
For her to buy a guitar which costs ( c ), she must have the same amount in her savings account ( T ). We will equate the two and solve for ( x ) to determine the minimum number of weeks required for her to save the cost of a guitar:
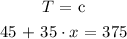
We have a single variable equation which can be solved by algebraic manipulation as follows:
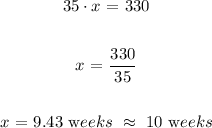
Therefore, she