Question

f(x) = x-3, g(x) = 6x-7, h(x) = 2 (to the power x)a) work our the value of x when f(x) = 0.5b) Fing g inverse (2)c) work out the value of x when h(x) = f(11)

Answer 1

The given functions are

`\begin{gathered} f(x)=x-3 \\ \\ g(x)=6x-7 \\ \\ h(x)=2^x \end{gathered}`

a)

Since f(x) = 0.5

Then equate x - 3 by 0.5

`x-3=0.5`

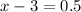
Add 3 to both sides

`\begin{gathered} x-3+3=0.5+3 \\ x=3.5 \end{gathered}`

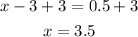
The value of x is 3.5

b)

To find the inverse of g do these steps

1. Replace g(x) by y

`y=6x-7`

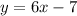
2. Switch x and y

`x=6y-7`

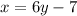
3. Solve to find y

`\begin{gathered} x+7=6y-7+7 \\ x+7=6y \\ (x+7)/(6)=y \\ \\ y=(x+7)/(6) \end{gathered}`

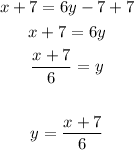
4. Replace y by g^(-1)

`g^(-1)(x)=(x+7)/(6)`

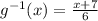
Substitute x by 2

`g^(-1)(2)=(2+7)/(6)=(9)/(6)=(3)/(2)=1.5`

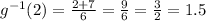
The value of g inverse of 2 is 1.5

c)

Find at first f(11)

`\begin{gathered} f(11)=11-3 \\ f(11)=8 \end{gathered}`

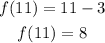
Equate h(x) by 8

`2^x=8`

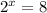
Since 8 = 2 x 2 x 2, then

`8=2^3`

Replace 8 by 2^3

`2^x=2^3`

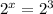
By using the rule of equal bases (their powers are equal), then

`x=3`

The value of x is 3