In order to determine the time the rocket takes to hit the ground, use the following formula for free fall when an object is launches:
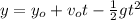
where,
vo: initial velocity = 15m/s
yo: initial height = 3m
g: gravitational acceleration constant = 9.8 m/s^2
y: final height = 0 m (the rocket is on the ground)
Replace the previous values into the equation above and order the equation as a quadratic equation in standard form:
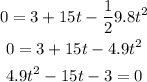
Next, use the quadratic formula, with a = 4.6, b = 15 and c = -3, to find the solutions for t:
![\begin{gathered} t=\frac{-(-15)\pm\sqrt[]{15^2-4(4.9)(-3)}}{2(4.9)} \\ t=(15\pm16.85)/(9.8) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/3vce3yeitbyahh4bgxoqpehv6vj5st0zyz.png)
take the positive solution for t (because negative times does not have physical meaning), then:
t = (15 + 16.85)/9.8 = 3.25 s
Hence, the rocket takes approximately 3.25 s to hit the ground