Question

Sophie is designing a logo withthree lines, y, m, and n. Line mpasses through point (-2,-1) andis perpendicular to the graph ofy = {x+6. Line n is parallel toline m and passes through thepoint (4, -3). What is the equationin slope-intercept form of line n?

Answer 1

Step 1

State a known relationship between the slopes of perpendicular lines

`\begin{gathered} \text{let m}_1=\text{ slope of line 1} \\ \text{and} \\ m_2=\text{ slope of line 2} \\ \text{Then} \\ m_2=(-1)/(m_1) \end{gathered}`

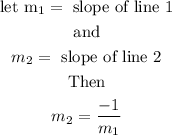
Step 2

Find the equation of line m using the above slope relationship

`\begin{gathered} \text{The equation of a line is in the form of} \\ y\text{ =mx +c} \\ \text{where} \\ m\text{ = slope} \\ c\text{ = y-intercept} \\ Line\text{ y has an equation of} \\ y\text{ =-}(2)/(3)\text{x+6 } \\ so\text{ that } \\ m\text{ =-}(2)/(3) \\ y=6 \end{gathered}`

Therefore,

`\begin{gathered} m_1=-(2)/(3) \\ m_2=(-1)/(-(2)/(3)) \\ m_2=-1*-(3)/(2) \\ m_2=(3)/(2) \\ so\text{ line m has aslope of }(3)/(2) \end{gathered}`

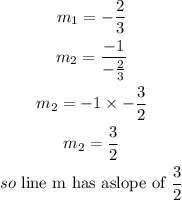
Line m passes through points (-2,-1) in the form of (x,y)

Therefore, the equation of line m will look like

`\begin{gathered} y\text{ =}(3)/(2)x\text{ + c} \\ \text{if x = -2 and y =-1} \\ \text{Substituting yields} \\ -1\text{ = }(3)/(2)(-2)\text{ +c} \\ -1\text{ = -3+c} \\ c\text{ = -1 +3} \\ \text{c = 2} \\ So\text{ the equation of line m will be} \\ y\text{ = }(3)/(2)x\text{ +2} \end{gathered}`

Step 3

Write a relationship between parallel lines n and m that will enable us to get the equation of line n

`\begin{gathered} \text{For parallel lines},\text{ slope are equal} \\ \text{let the slope of line n be m}_3 \\ \text{Then} \\ m_2=m_3 \\ \text{Therefore,} \\ m_3=(3)/(2) \end{gathered}`

Line n passes through points ( 4, -3), for (x,y)

Hence line n's equation will look like

`\begin{gathered} y\text{ =}(3)/(2)x\text{ + c} \\ y=-3 \\ x=4 \\ \text{Substituting} \\ -3\text{ = }(3)/(2)(4)+c \\ -3\text{ =}6+c \\ \text{c = -3-6} \\ c=\text{ -9} \\ \text{Hence the equation of line n is} \\ y\text{ =}(3)/(2)x\text{ -9} \end{gathered}`

The required equation of line n in slope-intercept form is

y =(3/2)x -9