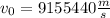Firstly, the force a charged particle feels when submited to an eletric field is:
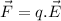
And, in our case, F will be:
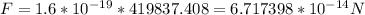
By using Newton's second law, we know that
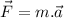
Then, we can find out our acceleration, which will be
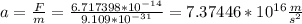
We now have the acceleration the electron would feel. We also know the distance it'll travel, which is 2.028mm. With this, we can apply Torricelli's equation, which tells us that:
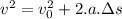
By isolating v0 we get
![v_0=\sqrt[2]{v^2-2.a.\Delta s}](https://img.qammunity.org/2023/formulas/physics/college/8vdmx5f2o7z9ioz255z9vnahd5awmd6ue9.png)
Finally, replacing our values, we get:
![v_0=\sqrt[2]{14672627.552^2-2*7.37446*10^(16)*2.028*10^(-3)}](https://img.qammunity.org/2023/formulas/physics/college/cfc68c7uafrr6ryb1kmp9p4hkv4erzov6u.png)
Then