Question

Solve this system of equations:{x + y = 5}{x2 + y2= 25}

Answer 1

We have the system of equations:

`\begin{gathered} x+y=5 \\ x^2+y^2=25_{} \end{gathered}`

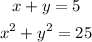
We can clear y from the first equation and replace it in the second:

`x+y=5\longrightarrow y=5-x`
`\begin{gathered} x^2+y^2=25 \\ x^2+(5-x)^2=25 \\ x^2+(25-10x+x^2)=25 \\ 2x^2-10x+25=25 \\ 2x^2-10x=25-25 \\ 2x^2-10x=0 \\ x^2-5x=(0)/(2) \\ x(x-5)=0 \\ x_1=0 \\ x_2=5 \end{gathered}`

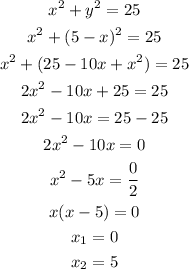
We have two solutions for x: x1=0 and x2=5.

Then, we can calculate the solutions for y:

`\begin{gathered} y_1=5-x_1=5-0=5 \\ y_2=5-x_2=5-5=0 \end{gathered}`

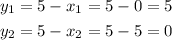
Then, the solutions are (0,5) and (5,0).

Answer: We have two solutions. One solution is x=0 and y=5 and the other solution is x=5 and y=0.