Question

An assessment has 20 questions for a total value of 100 points. The test consists of true/false questions worth 3 points each and multiple-choice questions worth 11 points each.How many multiple-choice questions and true/false questions are on the assessment?

Answer 1

The Solution:

Let the number of True/False questions in the assessment be represented with x.

And the number of multiple-choice questions be represented with y.

Given that the total number of questions is 20.

We have,

`x+y=20\ldots\text{eqn}(1)`

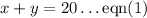
Given that each True/False question is worth 3 points while each multiple-choice question is worth 11 points and the total value of the whole question is 100 points.

We have,

`3x+11y=100\ldots\text{eqn}(2)`

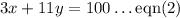
We are required to find the number of the True/False questions (x) and the number of multiple-choice questions (y).

Solving the eqn(1) and eqn(2) simultaneously by the Substitution Method, we have from eqn(1) that:

`y=20-x\ldots\text{eqn}(3)`

Putting eqn(3) into eqn(2), we get

`\begin{gathered} 3x+11(20-x)=100 \\ 3x+220-11x=100 \end{gathered}`

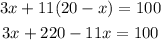
Collecting the like terms, we get

`\begin{gathered} 3x-11x=100-220 \\ -8x=-120 \end{gathered}`

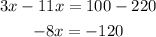
Dividing both sides by -8, we get

`x=(-120)/(-8)=15`

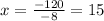
So, the number of True/False questions in the assessment is 15.

To find x, we shall substitute 15 for x in eqn(3)

`\begin{gathered} y=20-15 \\ y=5 \end{gathered}`

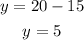
Thus, the assessment has 5 multiple-choice questions.