INFORMATION:
We have the next given information:
- Slope = -3
- point on the line: (1,4)
And we must find the equation that describes the line in slope-intercept form
STEP BY STEP EXPLANATION:
If we have the slope and a point and we need the slope-intercept form, we can write first the equation in point-slope form:

Where, (x1, y1) is the point on the line and m is the slope
Now, we have that
- Slope = -3
- point on the line: (1,4)
So, replacing the values in the formula
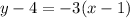
Finally, we must solve it for y to find the slope-intercept form of the line
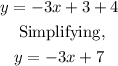
ANSWER:
the equation that describes the line in slope-intercept form with slope = -3 and passes through the point (1,4) is:
y = -3x + 7