To answer this question, we can see that we have a right triangle here. To find the length of the third side, we can apply the Pythagorean Theorem as follows:
![x^2+6^2=(2\sqrt[]{34})^2](https://img.qammunity.org/2023/formulas/mathematics/college/jhyvsizqdfm4z1iwg7lncxx10ve81tymu4.png)
Then, we have:
![x^2+36=2^2(\sqrt[]{34})^2](https://img.qammunity.org/2023/formulas/mathematics/college/38t6n6l7e438it2ie6nc3r4vboeyfzmwp1.png)
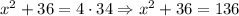
Therefore, if we subtract 36 from both sides of the equation, we have:
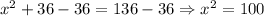
Finally, we have:
![\sqrt[]{x^2}=\pm\sqrt[]{100}\Rightarrow x=\pm10](https://img.qammunity.org/2023/formulas/mathematics/college/h25b3zdb338ov9bynhmw5oq8vuk0lue3u1.png)
Since the length of a triangle must be positive, then the value for the third side is 10.
In summary, w