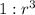Step-by-step explanation:
Linear escale factor 1.
In this case the original volume of the parallelepiped is:

24 cubic units and the new volume must be:
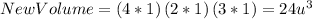
So in this case the ratio of volumes is 1:1
Linear escale factor 2.
In this case the original volume of the parallelepiped is the same: 24 cubic units.
The new voume must be:
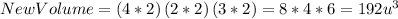
So in this case the ratio of volumes is 24:192, that is 1:8
Linear escale factor 3.
In this case the original volume of the parallelepiped is the same: 24 cubic units.
The new voume must be:
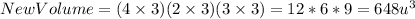
So in this case the ratio of volumes is 24:648, that is 1:27
Linear escale factor 4.
In this case the original volume of the parallelepiped is the same: 24 cubic units.
The new voume must be:
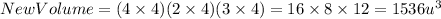
So in this case the ratio of volumes is 24:1536, that is 1:64
Linear escale factor r.
In this case the original volume of the parallelepiped is the same: 24 cubic units.
The new voume must be:

So in this case the ratio of volumes is 24:24r^3, that is: