Answer:
The value of the 17th term is;

Step-by-step explanation:
Given that;
For a given geometric sequence, the 9th term is equal to
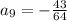
the 13th term, Q13, is equal to - 172.
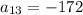
Recall that for geometric progression;
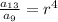
where r is the common ratio
substituting the given;
![\begin{gathered} r^4=(a_(13))/(a_9)=(-172)/((-(43)/(64))) \\ r^4=(-172)/((-(43)/(64)))=172*(64)/(43) \\ r^4=4*64 \\ r^4=256 \\ r=\sqrt[4]{256} \\ r=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ud0dkaeghsbmgrf0sw2yee9j4psp0wjooh.png)
To find the value of the 17th term;
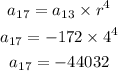
Therefore, the value of the 17th term is;
