You know that:
- Point R divides PQ in this ratio:
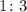
- The x-coordinate of Point R is:
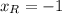
- The x-coordinate of Point P is:
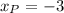
Then, you can make this drawing (it is not drawn to scale).
The Internal Section Formula for the x-coordinate of the point that divides the segment is:
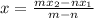
Where the coordinates of the endpoints are:

And the segment is divided internally in the ratio:

In this case, you can identify that:
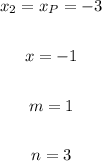
Then, you can substitute values and solve for:
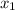
Which, in this case, is the x-coordinate of Point Q.
Then, you get:
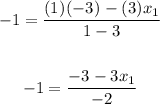
![undefined]()