Question

Find the measure of angle ARound your answer to the nearest tenth

Answer 1

In order to find the measure of angle A, we can use the sine relation of this angle.

The sine of a angle in a right triangle is equal the length of the opposite side to the angle over the length of the adjacent leg to the angle.

So we have that:

`\sin (A)=(5)/(13)`

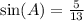
Now, using a calculator to find the inverse function of the sine, we have:

`\begin{gathered} \sin (A)=(5)/(13) \\ A=\sin ^(-1)((5)/(13)) \\ A=22.62\degree \end{gathered}`

So angle A is equal 22.62°.