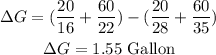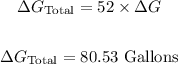Question

Question 15. Part A. Thank you so much for your help!

Answer 1

The first step to having a good solution in the present question, building an equation that gives us the number of Gallons (G) in the function of rate miles/gallons in the city (C) and miles/gallons in the highway (H).

We know that in typical weeks Jon drives 20miles in the city (Dc) and 60 miles on highway (Dh) (Going + Coming Back from his parent's house).

The rates of the number of gallons per mile are calculated as follows:

`\begin{gathered} C=(20)/(G_c)=\frac{\text{Distance}}{\text{Gallons used}}\to G_C=(20)/(C) \\ \\ H=(60)/(G_H)=\frac{\text{Distance}}{\text{Gallons used}}\to G_H=(60)/(H) \end{gathered}`

Anthe total number of gallons is equal to the sum of each case:

`\begin{gathered} G=G_H+G_C \\ \\ G=(20)/(C)+(60)/(H) \end{gathered}`

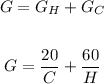
Now, to solve the problem, we just need to substitute the values as follows:

A - I)

The present car has the given rates:

`\begin{gathered} H=22\text{mpg} \\ C=16\text{mpg} \end{gathered}`

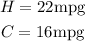
Substituting:

`\begin{gathered} G_1=(20)/(16)+(60)/(22) \\ G_1=1.25+2.73 \\ G_1=3.98\text{ Gallons} \end{gathered}`

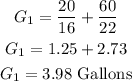
A-II)

The new values are:

`\begin{gathered} H=35\text{mpg} \\ C=28mpg \end{gathered}`

Substituting, we have:

`\begin{gathered} G_2=(20)/(28)+(60)/(35) \\ G_2=0.72+1.71 \\ \\ G_2=2,43\text{ Gallons} \end{gathered}`

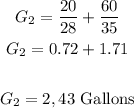
A-III

The difference for 52-week year is equal to the difference for a single week times 52, as it is calculated as follows:

`\begin{gathered} \Delta G=((20)/(16)+(60)/(22))-((20)/(28)+(60)/(35))_{} \\ \Delta G=1.55\text{ Gallon} \end{gathered}`
`\begin{gathered} \Delta G_{\text{Total}}=52*\Delta G \\ \\ \Delta G_{\text{Total}}=80.53\text{ Gallons} \end{gathered}`