To find the relative minimum and maximum, we need to find the derivative for the equation of the function:
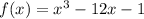
Then, the derivative is (following the rules of derivatives):
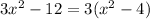
To find the relative maximum and minimum, we need to equate the derivative to zero, and solve for x:
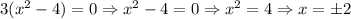
In this case, we have two values for x, x = -2, and x = 2.
Substituting these values in the original equation, we have:
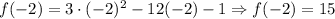
And
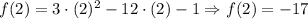
In this case, we have two pair of values:
(-2, 15), and (2, -17).
If we obtain the second derivative for the original value, we have that is 6x.
If we substitute x = -2 in the second derivative, we have 6 * (-2) = -12. Since the value is negative, the point (-2, 15) is a Relative Maximum.
Likewise, if we make x = 2, we have 6 * (2) = 12. Since this value is positive, we have a relative minimum (2, -17).
Therefore:
Relative maximum: (-2, 15).
Relative minimum: (2, -17).
So the correct option is the last one.