slope
Step-by-step explanation
Step 1
Fin the slope of the line:
the function
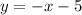
is written in the slope-intercept form:
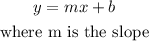
therefore, we can conclude
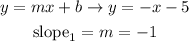
the solpe1 is -1
Now, we know that 2 lines are parallel if they have the same slope,
so
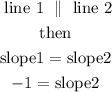
it means the slope of the line we are looking for is -1
Step 2
now, we have the slope and a point of the line, we can use
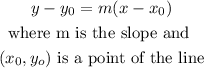
then, let's replace
let P(3,2)
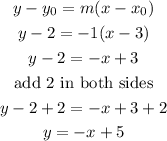
therefore, the equation is
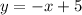
I hope this helps you