Given:
The solar power per unit surface of the earth is: P = 700 W/m²
The dimensions of the roof are: A = 8.83 m × 13.67 m
The time for which the solar radiation is incident on the roof is: t = 4.43 h
To find:
The energy incident on the roof.
Step-by-step explanation:
The area A of the roof is:

The time t can be converted into seconds as:

The energy incident on the given surface area in the given time is calculated as:

Substituting the values in the above equation, we get:
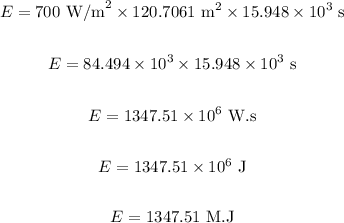
Final answer:
The amount of solar energy incident on the roof is 1347.51 Mega Joules (M.J)