The characteristics of the ellipse are as follows:
- The center is
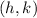 where
where
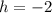 and
and
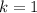 .
.
- The value for
 (the semi-minor axis) is approximately
(the semi-minor axis) is approximately
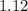 .
.
- The value for
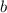 (the semi-major axis) is approximately
(the semi-major axis) is approximately
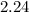 .
.
- The foci with the positive
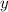 value is the point
value is the point
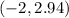 , rounded to two decimal places.
, rounded to two decimal places.
- The foci with the negative
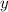 value is the point
value is the point
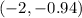 , rounded to two decimal places.
, rounded to two decimal places.
To write the given equation
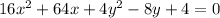 in standard form and determine the various characteristics of the conic section it represents, we will complete the square for both \(x\) and \(y\) terms. Here are the steps:
in standard form and determine the various characteristics of the conic section it represents, we will complete the square for both \(x\) and \(y\) terms. Here are the steps:
1. Group the
 and
and
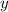 terms together:
terms together:
![\[ 16x^2 + 64x + 4y^2 - 8y = -4 \]](https://img.qammunity.org/2023/formulas/mathematics/college/frh1aqrcw1bxzfn5wmkducuz6v8k3qi3eb.png)
2. Factor out the coefficients of the squared terms from each group:
![\[ 16(x^2 + 4x) + 4(y^2 - 2y) = -4 \]](https://img.qammunity.org/2023/formulas/mathematics/college/8roaofm9wofz2exj8df4uobguqe99nachi.png)
3. Complete the square for the \(x\) terms and the \(y\) terms. This involves adding the square of half the coefficient of the \(x\) term inside the parentheses to both sides of the equation, and similarly for the \(y\) term:
![\[ 16(x^2 + 4x + (4/2)^2) + 4(y^2 - 2y + (2/2)^2) = -4 + 16(4/2)^2 + 4(2/2)^2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/2kvl8n7x4wuafx0v1xx8epinsn50fpi8dm.png)
4. Simplify and convert the equation into standard form:
![\[ 16(x + 2)^2 + 4(y - 1)^2 = 16 + 4 \]](https://img.qammunity.org/2023/formulas/mathematics/college/j8b1k2ygjgu7nk2a9gxmv8hfbysv9t1r8a.png)
5. Continue simplifying:
![\[ 16(x + 2)^2 + 4(y - 1)^2 = 20 \]](https://img.qammunity.org/2023/formulas/mathematics/college/t2juxrdq09r3ex62l7rmmrrv5p64tmrhtf.png)
6. Divide through by 20 to get the equation in standard form:
![\[ ((x + 2)^2)/(20/16) + ((y - 1)^2)/(20/4) = 1 \]](https://img.qammunity.org/2023/formulas/mathematics/college/olxnj6hintdrh6cezlcn0csnbq32b1jymt.png)
![\[ ((x + 2)^2)/(5/4) + ((y - 1)^2)/(5) = 1 \]](https://img.qammunity.org/2023/formulas/mathematics/college/srxs2xw0r2cnb9h5quesxpdbj6guhe4jcg.png)
The standard form of an ellipse is
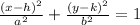 , which allows us to identify the center \((h, k)\), and the values of \(a\) and \(b\).
, which allows us to identify the center \((h, k)\), and the values of \(a\) and \(b\).
So, for our equation:
-
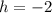
-
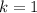
-
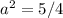 which gives us
which gives us
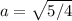
-
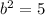 which gives us
which gives us
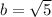
For the foci of an ellipse, which are located along the major axis, we use the relationship
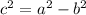 (or vice versa depending on which is larger). For this ellipse, since
(or vice versa depending on which is larger). For this ellipse, since
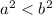 , we'll have
, we'll have
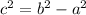 .
.
Let's calculate the exact values for
 ,
,
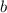 , and
, and
 , and then determine the coordinates of the foci.
, and then determine the coordinates of the foci.
The characteristics of the ellipse are as follows:
- The center is
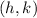 where
where
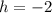 and
and
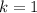 .
.
- The value for
 (the semi-minor axis) is approximately
(the semi-minor axis) is approximately
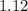 .
.
- The value for
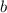 (the semi-major axis) is approximately
(the semi-major axis) is approximately
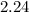 .
.
- The foci with the positive
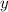 value is the point
value is the point
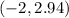 , rounded to two decimal places.
, rounded to two decimal places.
- The foci with the negative
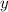 value is the point
value is the point
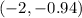 , rounded to two decimal places.
, rounded to two decimal places.