Question

There are 12 students in a class, and 5 of them will be chosen to go on a field trip. How many ways can these students be chosen?

Answer 1

792 ways

Explanation:

The number of students in the class = 12

If 5 of them are to go on the field trip, since the order doesn’t matter. the number of ways that these children could be chosen can be calculated using combination.

`^(12)C_5`

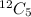
Recall:

`^nC_r=(n!)/((n-r)!r!)`

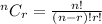
Therefore:

`\begin{gathered} ^(12)C_5=(12!)/((12-5)!5!) \\ =(12*11*10*9*8*7!)/(7!*5!) \\ =(12*11*10*9*8)/(5!) \\ =(12*11*10*9*8)/(5*4*3*2*1) \\ =(95040)/(120) \\ =792 \end{gathered}`

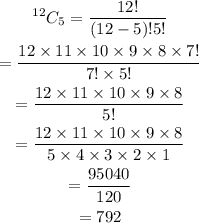
The students can be chosen in 792 ways.