(a) Height at which the ball is shot from the canon
Write the equation of the height as a function of time.
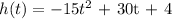
The initial height of the ball is the height at time t =0.
Hence:
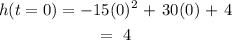
(b) Time at which the ball reaches the maximum height
We can obtain this by differentiating h(t) with respect to t, and then equating the expression to zero.
Taking the first derivative:
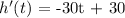
Equating the zero:
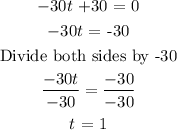
The ball reaches maximum height at t = 1s
(c) The maximum height the ball can reach
Substituting 1 for t into the expression h(t):
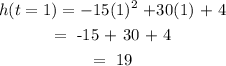
The maximum height the ball can reach is 19ft
(d) How long for the ball to reach the ground
The ball would reach the ground at exactly 2 times the value it takes to reach the maximum height
Hence:
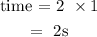
It would take 2s for the ball to reach the ground