Question

Determine whether the parallelogram with the given vertices is a rectangle, rhombus , or square. Give all names that apply. Explain your reasoning. You must use properties of diagonals to show and explain your reasoning. A(-6,-2)B (-3,3) C (2,0)D (-1,-5)

Answer 1

We will have the following:

First, we have the graph of the problem:

Now, we determine the slope of the diagonals, and if those are perpendiullar we then have that it will be a square, that is:

`\begin{cases}m_(AC)=(0-(-2))/(2-(-6))\Rightarrow m_(AC)=(1)/(4) \\ \\ m_(BD)=(-5-3)/(-1-(-3)))\Rightarrow m_(BD)=-4\end{cases}`

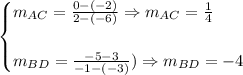
From this, we can see that the slopes are perpendicular. This is a condition for a square or a rhombus.

Now, we determine if the graph belongs to a square by determining if the slopes of AB & BC are perpendicular:

`\begin{cases}m_(AB)=(3-(-2))/(-3-(-6))\Rightarrow m_(AB)=(5)/(3) \\ \\ m_(BC)=(0-3)/(2-(-3))\Rightarrow m_(BC)=-(3)/(5)\end{cases}`

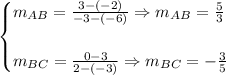
From this we can see that those segmens are also perpendicular, so in this particular case the graph is a square. [Which technically speaking is also a rhombus].

The reasoning is that the diagonals are perpendicular and the external segments are also perpendicular, a property that belong to squares.

Now, we find the intersection point of the diagonals, that is:

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))_{}`

`M((2-6)/(2),(0-2)/(2))\rightarrow M(-2,-1)`

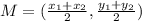
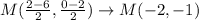
Now, we determine the distance of all 4 segments AM, BM, CM & DM:

`\begin{cases}d_(AM)=\sqrt[]{(-2+6)^2+(-1+2)^2}\Rightarrow d_(AM)=\sqrt[]{17} \\ \\ d_(BM)=\sqrt[]{(-2+3)^2+(-1-3)^2}\Rightarrow d_(AM)=\sqrt[]{17} \\ \\ d_(CM)=\sqrt[]{(-2-2)^2+(-1-0)^2}\Rightarrow d_(CM)=\sqrt[]{17} \\ \\ d_(DM)=\sqrt[]{(-2+1)^2+(-1+5)^2}\Rightarrow d_(DM)=\sqrt[]{17}\end{cases}`

So, the distance of all segments that divide the diagonals are equal, thus the points describe a square.