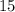Answer:
The number of handshakes that will be there is;
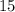
Step-by-step explanation:
Given that there are 6 people in the party.
And each person must shake hands with every other person exactly once.
So, since order is not improtant, we have;
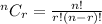
For this question;
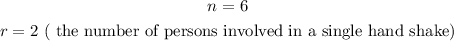
It then becomes;
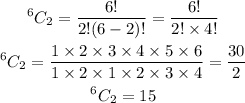
Therefore, the number of handshakes that will be there is;