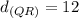1 Answer

Osoner · Answer 1 · 2023-07-24T10:08:22+0000

For this exercise you need to use the formula for calculate the distance between two points:

$d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}$

In this case you know that the points are:

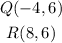
$\begin{gathered} Q\mleft(-4,6\mright) \\ R(8,6) \end{gathered}$

So you can set up that:

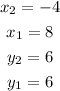
$\begin{gathered} x_2=-4 \\ x_1=8 \\ y_2=6 \\ y_1=6 \end{gathered}$

Substitute the corresponding coordinates into the formula and then evaluate, in order to find the distance from point Q to point R:

$\begin{gathered} d_((QR))=\sqrt[]{(-4-8)^2+(6-6)^2} \\ d_((QR))=\sqrt[]{(-12)^2+(0)^2} \\ d_((QR))=\sqrt[]{144} \\ d_((QR))=12 \end{gathered}$

The answer is;

Please log in or register to add a comment.