Answer:
A. The solution to the system of equations is (2, -4, 3)
Explanation:
Given the system of linear equations:
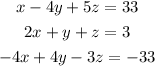
The row matrix for the system is given below:
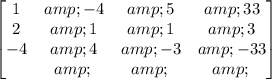
We perform the row operations below to solve for x, y and z.
Step 1: Multiply R2 by 1/2:
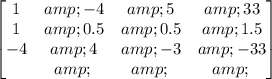
Step 2: Multiply R3 by -1/4:
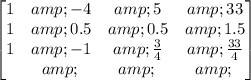
Step 3: Carry out the operation: R2-R1-->R2
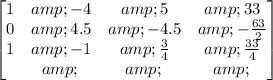
Step 4: Carry out the operation: R3-R1-->R3
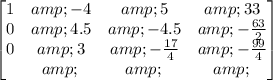
Step 5: Multiply R2 by 2/9.
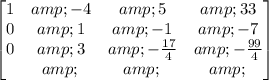
Step 6: Multiply R3 by 1/3:
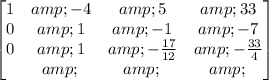
Step 7: Subtract R2 from R3
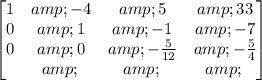
Step 8: Multiply R3 by -12/5.
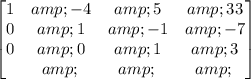
Step 9: Add R2 to R3 on R2:
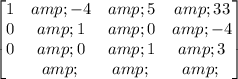
Step 10: Perform the operation: R1-5R3 on Row 1.
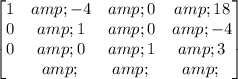
Step 11: Perform the operation: R1+4R2 on Row 1.
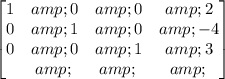
We see that the identity 3 x 3 matrix is formed on the left.
Therefore, the solution to the system of equations is:
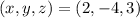
Option A is correct.