Question

Hello, could you help me with this problem I don't understand it

Answer 1

We have 3 line equations.

`\begin{gathered} l_1\colon2x-8y=-24 \\ l_2\colon4x+y=-2 \\ l_3\colon x-4y=4 \end{gathered}`

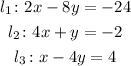
To check if the lines are parallel, perpendicular or neither, we need to check their slopes. If the slopes are equal, the lines are parallel, if the slope of one of the lines is equal to minus the inverse of the other slope, the lines are perpendicular, and finally, if any of those statements is not fullfilled, they are neither.

To find the slope of each line equation, let's rewrite all of them in slope-intercept form.

The slope-intercept form is

`y=mx+b`

Where m represents the slope and b the y-intercept.

Now, let's rewrite our equations.

For the first line we have:

`\begin{gathered} 2x-8y=-24 \\ x-4y=-12 \\ -4y=-x-12 \\ 4y=x+12 \\ y=(x)/(4)+3 \end{gathered}`

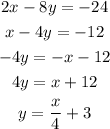
For the second we have:

`\begin{gathered} 4x+y=-2 \\ y=-4x-2 \end{gathered}`

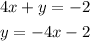
And finally, for the third:

`\begin{gathered} x-4y=-4 \\ -4y=-x-4 \\ y=(x)/(4)+1 \end{gathered}`

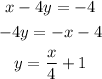
Our lines in slope intercept form are:

`\begin{gathered} l_1\colon y=(x)/(4)+3 \\ l_2\colon y=-4x-2 \\ l_3\colon y=(x)/(4)+1 \end{gathered}`

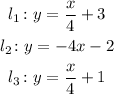
The slopes are, respectively

`m_1=(1)/(4),m_2=-4,m_3=(1)/(4)`

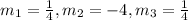
Since

`m_1=-(1)/(m_2)=m_3`

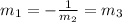
We have

`\begin{gathered} l_1\parallel l_3 \\ l_1\perp l_2 \\ l_2\perp l_3 \end{gathered}`

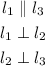
2x - 8y = -24 and x - 4y = 4 are parallel;

2x - 8y = -24 and 4x + y = -2 are perpendicular;

x - 4y = 4 and 4x + y = -2 are perpendicular.