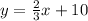We are given the equation
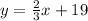
and the point (-9,4). We want to find the equation of a line of the form

that is parallel to the given line and passes through the given point. Note that, two lines are parallel if and only if they have the same slope. So, in this case, we should find the value of m for the first line equation. By comparison, we can check that the slope of the first equation is 2/3. So, this means that the slope of the second equation (m) should be 2/3 also. So our equation looks like this
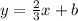
since we want this equation to pass through the point (-9,4) this means that whenever we replace x by -9, we should replace y by 4. So we get the following equation
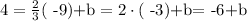
So, if we add 6 on both sides, we get

so the equation of the line at is parallel to the original line and that passes through the given point is