Question

4. It is the ratio of the length of the hypotenuse to the length of the side adjacent to the given angle in a right triangle. A. cosecant B. cosine C. cotangentD. secant

Answer 1

We can see from the question that we are dealing with trigonometric ratios here. We have a right triangle, and we have to find the ratio between:

• The length of the hypotenuse to the length of the side adjacent to the given angle

1. To find it, we can graph a right triangle as follows:

2. Then we have that the reference angle here is Θ, and we can see that the adjacent side to it is a, and the hypotenuse is the side in front of the right angle.

3. From the definition of the trigonometric ratios, we have that:

`cos(\theta)=\frac{\text{ Adjacent side}}{\text{ Hypotenuse}}=(a)/(h)(\text{ In the graph\rparen}`

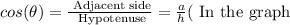
4. And we have that the ratio of the length of the hypotenuse to the length of the side adjacent to the given angle in a right triangle is the inverse of the latter ratio, and is defined as follows:

`sec(\theta)=\frac{\text{ Hypotenuse}}{\text{ Adjacent side}}=(h)/(a)(\text{ From the graph\rparen}`

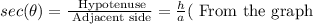
And this is the secant ratio.

Therefore, in summary, we can conclude that the ratio of the length of the hypotenuse to the length of the side adjacent to the given angle in a right triangle is the secant (Option D).