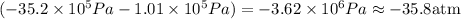Question

Can you please help i cant seem to find the answer

Answer 1

ANSWERS

1. 13 m³

2. v2 = 86.25 m/s

3. -35.8 atm

Step-by-step explanation

1. The volume of water flowing in a 8min period is

`V=v_1\cdot t\cdot A_1`

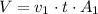
Where v1 = 13.8m/s, t = 8min and A1 is the section of the pipe:

`A_1=\pi\cdot r^2=(\pi)/(4)d^2_1`

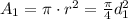
So the volume is (remember to transform the time from minutes to seconds and the diameter from centimeters to meters)

`V=13.8(m)/(s)\cdot8\min \cdot(60s)/(1\min)\cdot(\pi)/(4)\cdot0.05^2m^2`
`V=13.8(m)/(s)\cdot480s\cdot0.00196m^2`
`V\approx13m^3`

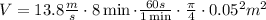
2. The speed in the left section of the pipe is

`v_2=v_1\cdot(A_1)/(A_2)`

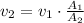
This is because the flow rate is constant along the pipe (Q = v*A).

As shown in the previous item the area is

`A=(\pi)/(4)\cdot d^2`

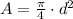
So when dividing both areas the factor π/4 cancels out. Therefore the speed is

`v_2=v_1\cdot(d^2_1)/(d^2_2)`

In this case we can use centimeters for the diameters because in the division the units cancel out

3. Using Bernoulli's equation:

`p_1+(1)/(2)\cdot\rho\cdot v^2_1+\rho\cdot g\cdot h_1=p_2+(1)/(2)\cdot\rho\cdot v^2_2+\rho\cdot g\cdot h_2_{}`

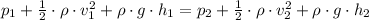
The pipe is horizontal so h1 = h2. Also, the pipe is open on the right side p1 = p0, where p0 is atmosferic pressure. The third term on each side of the equation cancels out because they are equal:

`p_0+(1)/(2)\cdot\rho\cdot v^2_1=p_2+(1)/(2)\cdot\rho\cdot v^2_2`

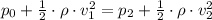
Solving for p2:

`p_2=p_0+(1)/(2)\cdot\rho\cdot v^2_1-(1)/(2)\cdot\rho\cdot v^2_2`

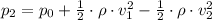
1/2 and ρ are common factors:

`p_2=p_0+(1)/(2)\cdot\rho(v^2_1-v^2_2)`

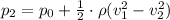
Atmosferic pressure is given 1.01x10⁵ Pa, ρ is also given 1000 kg/m³. The speeds are v1 = 13.8m/s and v2 = 86.25 m/s. The pressure in the left section of the pipe is

`p_2=-3.52*10^6Pa`

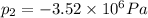
Thus, the guage pressure in the left section of the pope is:

`(-35.2*10^5Pa-1.01*10^5Pa)=-3.62*10^6Pa\approx-35.8\text{atm}`