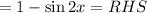Given the identity:

The proof of the identity will be as follows:
We will begin from the left-hand side by expanding the square

Combine the first and the last terms, which will be the Pythagorean identity

Note, note the last term (2 sin x cos x) = sin 2x
So,