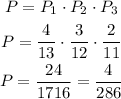Answer:
D) 4/286
Step-by-step explanation:
Let's organize the data in a table:
Number of coins Value of Coin
6 2$
4 5$
3 1$
Total: 13 coins
The probability one randomly selected coin is a 5$ dolar coin is:
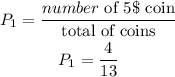
After this, there will be 12 remaining coins (and three 5$ coins).
So, the probability that the second coin is a $5 coin:
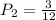
After this, there will be 11 remaining coins (and two 5$ coins).
So, the probability that the third coin is a $5 coin:

So, the probability that the three coins are 5$ coins is the product of the three coins.